Historia de los números imaginarios

Surgimiento de los números imaginarios

Su nombre fue acuñado por René Descartesen el Siglo XVII y lo propuso con intenciones despectivas aunque es un concepto válido, suponiendo un plano con ejes cartesianos en el que los números reales se encuentran sobre el eje horizontal y los imaginarios sobre el eje vertical complejo.
Para agregarle mitología además de llamarlo número imaginario, se le hizo pertenecer al conjunto de los números complejos. Si no conocemos el valor real de i, por lo menos sí sabemos que i elevada a la potencia i es un número irracionalconocido como: I = ii, por ejemplo: I = ii = 0,20787958140365… y este es un número imaginario que es muy real.

Historia

En el año 1777, Leonhard Euler le dio el nombre de i, por imaginario, de manera despectiva (i = √¯-1) dando a entender que no tenían una existencia real.
Gottfried Wilhelm Leibniz, en el siglo XVII, expresó "El Espíritu divino se manifestó sublimemente en esta maravilla del análisis, en este portento del mundo de las ideas, este anfibio entre el ser y el no ser, que llamamos raíz imaginaria de la unidad negativa".
En 1572, Rafael Bombelli ya había realizado cálculos utilizando números imaginarios pero sin utilizar aún la letra i, y en 1811, Jean-Robert Argand crea la representación gráfica del Plano complejo también conocida como plano de Argand.

Notación de un número imaginario

Numeros imaginarios 1.jpg
Un número imaginario se denota por bi, donde: bes un número real e i es la unidad imaginaria: √¯-1 = a i. Cada número imaginario puede ser escrito también como i·r donde r es un número real e i es la unidad imaginaria.
Los valores de las potencias de la unidad imaginaria se repiten de cuatro en cuatro. Los números imaginarios permiten calcular raíces con índice par y radicando negativo.

Recuperado de:
https://www.ecured.cu/Números_imaginarios

 Aslic Valenzuela 

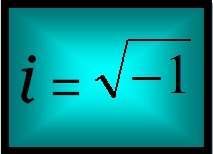
Comentarios

Publicar un comentario

Entradas populares de este blog

Relaciones de Conjuntos

Imagen
Relaciones entre conjuntos y elementos Relación de pertenencia Para comenzar, debes comprender la relación entre los  conjuntos  y los  elementos  que lo conforman.  Cuando un objeto es uno de los elementos de un conjunto decimos que  pertenece  al conjunto. Como has visto, es posible representar gráficamente la relación de pertenencia por medio de  diagramas de Venn  dibujando el elemento dentro de un circulo que representa el conjunto.  Ahora aprenderás a representar esta relación por medio de símbolos matemáticos. Se usa el símbolo que se muestra en la parte izquierda de la siguiente figura, como el  símbolo de la pertenencia .  Si queremos representar que cierto objeto  no pertenece  a determinado conjunto, usaremos el mismo símbolo atravesado por una línea, como se muestra en la figura de abajo a la derecha. En el ejemplo de abajo puedes ver el  conjunto unitario   , el cual está conformado por el elemento  .  Los símbolos del lado derecho representan de forma escri
Leer más
Imagen
Pendiente de una recta Primero necesitamos una forma de medir la “inclinación” de una recta, o cuál es la rapidez con la que sube (o baja) cuando pasamos de izquierda a derecha. Definimos el corrimiento como la distancia que nos movemos a la derecha y la elevación como la distancia correspondiente que la recta sube (o baja). La pendiente de una recta es la relación entre la elevación y el corrimiento: Pendiente = elevación/ corrimiento La Figura 1 muestra situaciones en las que la pendiente es importante. Los carpinteros usan el término inclinación para la pendiente de un techo o una escalera; el término pendiente se usa para la pendiente de una carretera. Si una recta está en un plano de coordenadas, entonces el corrimiento es el cambio en la coordenada x y la elevación es el cambio correspondiente en la coordenada y entre cualesquier dos puntos sobre la recta (vea Figura 2). Esto nos da la siguiente definición de pendiente. Referencias:  (2012). En J. St
Leer más

Las Funciones trigonométricas y sus gráficas

Imagen
Variación y gráficas de las funciones trigonométricas (seno, coseno, tangente, cotangente, secante y cosecante) Las funciones trigonométricas de un triángulo rectángulo son las razones o relaciones entre sus lados. Las funciones trigonométricas son algunas aplicaciones que nos ayudan en la resolución de triángulos rectángulos. Un triángulo tiene seis elementos: tres lados y tres ángulos. Resolver un triángulo consiste en calcular tres de los elementos cuando se conocen los otros tres, siempre que uno de ellos sea un lado. Gráficas de las funciones trigonométricas Si queremos representar en forma gráfica una función trigonométrica tomamos los valores de la variable independiente como abscisas y los valores de la función como ordenadas, obteniendo así una serie de puntos, los que al unirlos nos dará una línea que será la representación gráfica de la función. Uso de la función seno:  ésta se usa cuando en un triángulo rectángulo se conoce un ángulo agudo y el cateto opu
Leer más